Understanding Diffusion Models

I was asked about Diffusion Models in a generative AI intern interview. Honestly, I did not have much grip on it as I would have loved to at the moment. All I knew was it had to do something with pixels and noise. (Would've been pog if I checked above and beyond on Image GenAI advancements when I was learning about autoencoders in college but we cannot undo things now)

Diffusion models have revolutionized the field of generative artificial intelligence, particularly in image synthesis. These models have gained immense popularity due to their ability to generate high-quality, diverse images.

Diffusion models, as I speak now is the SOTA architecture to generate high quality images.

So that leaves us with ... what are Diffusion models afterall?

What are Diffusion Models?

Diffusion models are a class of generative models that learn to reverse a noise corruption process in the same way Joan Garcia tries to undo the Haram defence thanks to the likes of Araujo (diffuser). It kinda reminds me of how we always have a state of order for the first 15-20 minutes versus Celta Vigo and suddenly we are 2-0 down thanks to Iago Aspas, only to get back up again only because of my boy Rapha.

The Core Concept

The fundamental principle behind diffusion models is:

Forward Process (Noising): Gradually add noise to clean data until it becomes pure noise. Like pure pure noise.
Reverse Process (Denoising): Learn to reverse this process to generate clean data from noise

Figure 1: The forward diffusion process gradually adds noise to clean data

Figure 2: The reverse process learns to denoise and generate clean images

Mathematical Foundation

Forward Diffusion Process

The forward process is defined as a Markov chain that gradually adds Gaussian noise to the data:

q(x_t | x_{t-1}) = N(x_t; √(1-β_t) x_{t-1}, β_t I)

Where:

β_t is the noise schedule
x_t represents the data at timestep t
I is the identity matrix

Reverse Diffusion Process

The reverse process learns to denoise the data:

p_θ(x_{t-1} | x_t) = N(x_{t-1}; μ_θ(x_t, t), Σ_θ(x_t, t))

The neural network learns to predict the noise that was added at each timestep.

Understand it as the Manager trying to figure out the fault which caused the team to go 2-0 down. To get to the solution you have to get to the problem (the noise) which caused the opponent to score a goal at given minutes.

Popular Diffusion Model Architectures

DDPM (Denoising Diffusion Probabilistic Models)

The foundational paper that popularized diffusion models
Uses a U-Net architecture for noise prediction
Introduced the concept of noise scheduling

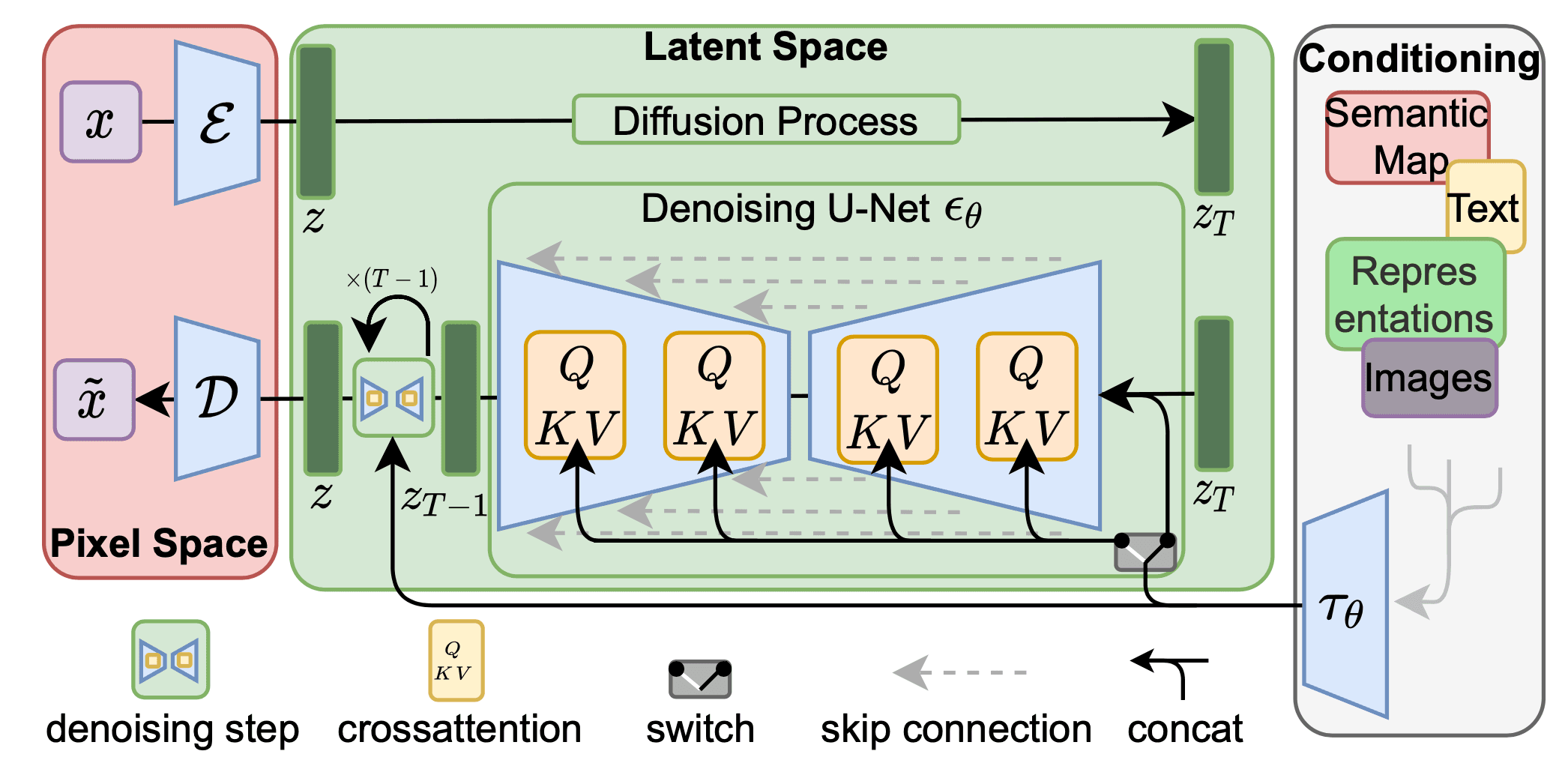Figure 3: DDPM uses a U-Net to predict noise at each timestep

Conclusion

Diffusion models represent a significant breakthrough in generative AI, offering a powerful and flexible framework for creating high-quality synthetic data. While they come with computational challenges, ongoing research continues to address these limitations and expand their capabilities.

As the field matures, we can expect to see even more impressive applications and improvements in efficiency, making diffusion models an essential tool in the AI toolkit.

This post provides a generic introduction to diffusion models. There is still a lot to type and document over here, but I plan to make a project delving deep into the mathematical aspect of diffusion models